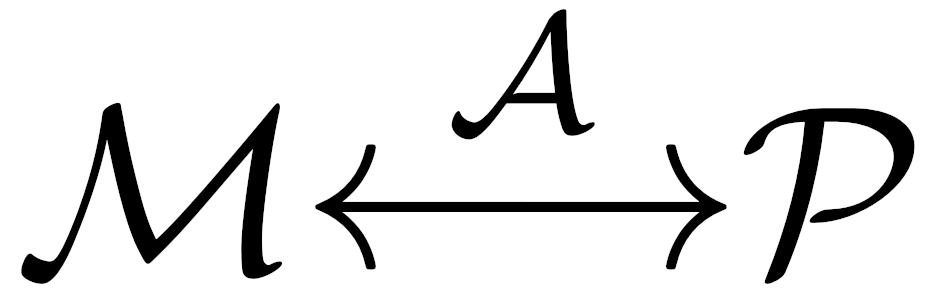Meeting Notes 2024-03-19

This Week’s Finds

We had quite a few interesting finds this week.

Riemann Tensor Symmetry Group (Again!)

Jim presented updated work that describes the symmetry group of the Riemann Tensor fully, without additional structure. The result creates a subset of the Young Symmetrizer group for the partition 2 + 2, which recovers all the index symmetries (and anti symmetries). An interesting note, this work found that the statement on Wikipedia to be incorrect, “The algebraic symmetries are also equivalent to saying that R belongs to the image of the Young symmetrizer corresponding to the partition 2+2.” As the image of Y(2 + 2) has symmetries in every pair of indices. More detail on this topic will be posted soon. [1]

 

Cyclic Groups and Infinitesimal Generators

Joshua posed the question, mostly about conventional use of terminology, “Could U(1) be considered a cyclic group?” The question is motivated by the notion of generators that are common across discrete and continuous groups. For example, the additive group \(\mathbb{Z}_n = \langle 1 \rangle\) is generated by a single element with the property \(1^n = 0\). The Lie group \(U(1)\) has generator-like object of an “infinitesimal rotation”. More concretely, the Lie algebra \(\mathfrak{u}(1)\) has a generator of an infinitesimal translation, which when exponentiated can recover a local patch of the group (locally isomorphic). The consensus seemed to be that the similarities were interesting, but did not merit the application of the term “cyclic” to the continuous case of groups like \(U(1)\). [2]

 

Measuring the Flatness of a Surface

Lael was asked by a machinist colleague if there was a well-behaved mathematical notion of “flat” as pertaining to a surface \(S\). Specifically, he was asked if there was a quantity \(f(S)\) that, when approaching \(0\) would indicate that the surface was reflective (or a “good” mirror). Lael introduced several possible measures, including sum of squares of height residuals, arc length vs. projected length, and others. The nature of reflectivity of a material was also discussed, and it was agreed that the condition needed to be local, not global.

 

Focus Session:

Reading summary.

 

Smooth Structures

We briefly summarized the notion of a smooth structure on a manifold and gave concrete examples. Specifically, a smooth structure on a manifold \(\mathcal{M}\) is a maximal smooth atlas \(\mathcal{A}\) on \(\mathcal{M}\), which is essentially a collection of all smooth charts \(\varphi \in C^\infty(\mathcal{M}): \mathcal{M} \to \mathbb{R}^n\) that are mutually smoothly compatible, or agree on any overlap. Note that these structures are not unique. Several examples of smooth manifolds were given (of the many given in Lee), including Grassman manifolds \(G_k(V)\), projective spaces $latex \mathbb{RP}^n, and others. Kokkimidis gave a brief overview of how Grassman manifolds are used in amplitudes research, by decomposing graphs into simpler pictures, coloring, and gluing over a chosen phase space. [3]

 

Subgroup Lattices and Planarity

We reviewed the notion of a lattice on a partially-ordered set, then looked at the case where the partial order is given by the subgroup relation. The question was posed, “is there a way to tell if a group possesses a subgroup lattice that is planar?” While no specific result for a group was given, Sangjun and Lael explained that for any finite graph, the graph is planar if and only if it does not contain a subgraph that is a subdivision of \(K_5\) (the complete graph of 5 vertices) or \(K_{3,3}\) (a complete bipartite graph on six vertices, three connecting to three). This result is know as Kuratowski’s theorem. [4]

 

Up Next:

Interesting or Relevant Talks:

• Math Colloquium

References:

1. Riemann Tensor Symmetries: https://en.wikipedia.org/wiki/Riemann_curvature_tensor#Symmetries_and_identities
2. U(1) Group: https://en.wikipedia.org/wiki/Circle_group
3. Bourjaily, Grassmannian Geometry of Scattering Amplitudes: https://www.cambridge.org/core/books/grassmannian-geometry-of-scattering-amplitudes/8820C87DD0B4F11D33BCD435D2A1F305
4. Kuratowski’s theorem: https://en.wikipedia.org/wiki/Kuratowski%27s_theorem