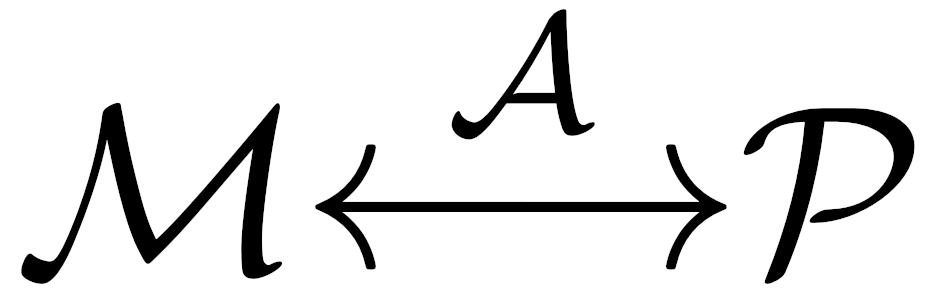Meeting Notes 2024-04-16

This Week’s Finds

We had quite a few interesting finds this week.

Heaviside Kernels and Physical Solutions

Joshua introduced the the question of choice of kernel function, sometimes called a window function, arising from integrals with infinite support in QFT. The technique is more broadly one that translates an integral over an unbounded domain to one of functions with finite support, allowing for use of local / global identities. The general case of a convergent series was discussed, with example kernels of Heaviside and a smooth exponential kernel. The sum \(\sum_{n=1}^\infty k(n) x_n\), where different choices for the kernel \(k(n)\) were discussed. For example, a Heaviside kernel can be defined for finite support \(N\), as \(k(n) = \Theta(N-n)\), which transforms the infinite sum into a limit of a finite sum \(\sum_{n=1}^\infty k(n) x_n = \lim_{N\to\infty} \sum_{n=1}^\infty \Theta(N-n) x_n\). Alternatively, one could define a smooth kernel function for a truncation \(N\), such as \(k(n) = e^{-n/N}\cos(\omega t)\). In both cases the answer to the summation (or integral) is unchanged. The discussion then revolved around a preference for a smooth kernel over a discontinuous one, and why a discontinuous choice (e.g. Heaviside) could be the conventional choice.

 

Focus Session:

Review of Bundles and Application to QFT

 

Bundles and Gauge Bosons

Samarth and Joshua, with interactive assists from the group, reviewed the basics of bundles, principal bundles, as well as how they apply to QFT and gauge boson fields. In general, a bundle is a combination of three things: (1) a base space \(M\), (2) a total space \(E\), and (3) a surjective map \(\pi: E \to M\) called the projection. The inverse image in \(E\) of a point \(p \in M\) in the base space is called the fiber of \(\pi\) over \(p\). It is often the case that the total space is produced as a disjoint union of local structures in the base space, for example, the tangent bundle is a disjoint union of the tangent space at each point of the base space (the manifold).

Adding a little more structure, a fiber bundle is a bundle with one additional object, \(F\) called the fiber. Further, we impose the conditional of local triviality on the bundle, which essentially implies that each fiber of the projection \(\pi^{-1}(p)\) is homeomorphic (or diffeo, etc) to the fiber space \(F\).

Next, we add a symmetry group to the bundle. A principal-G bundle is a fiber bundle along with a topological group (often a Lie group) \(G\) as well as a continuous right action on the total space \(E \times G \to E\) that preserves the fibers of \(\pi\). This implies that each fiber of the projection will be homeomorphic (or diffeo, etc) to the group \(G\), which takes place of the fiber space. Last, we define a connection on this principal-G bundle, which essentially is a choice in horizontal behavior (how to connect nearby fibers) of the bundle.

As an example, electricity and magnetism can be fully described using bundles. Specifically, the base space is a Minkowski manifold \(\mathbb{R}^{1,3}\), the fiber group is the Lie group \(U(1)\), and the connection \(A\) can be defined in terms of the Faraday tensor field \(F_{\mu\nu}\), where \(\mathrm{d} A = F\).

 

Up Next:

Interesting or Relevant Talks:

• Colloquia

References:

1. Bundle: https://en.wikipedia.org/wiki/Bundle_(mathematics)
2. Fiber Bundle: https://en.wikipedia.org/wiki/Fiber_bundle
3. Principal Bundle: https://en.wikipedia.org/wiki/Principal_bundle
4. Gauge Theory: https://en.wikipedia.org/wiki/Gauge_theory