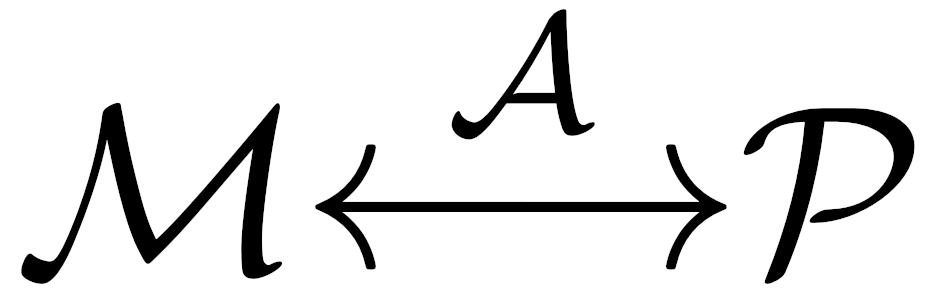Admin Items
- Feedback Survey
- Summer Survey
This Week’s Finds
We skipped finds this week to allow for a full focus session.
Focus Session:
Jim and Joshua presented on the application of this semester’s readings to cosmology, specifically on the definitions to homogeneity and isotropy. The goals of this presentation were to cover the Petrov classification of all 4-D spacetimes, as well as exploring the common example of FLRW cosmology.
Review of Readings \(+ \epsilon\)
We briefly reviewed our reading regarding smooth manifolds, including smooth functions, as well as group theory, including cosets and group orbits. We also introduced several new concepts, including: the metric, vectors, forms, and derivatives (to be examined in depth in summer), so that we could discuss Killing vectors.
Vectors, Forms, and Metrics. First, we introduce vectors as tangent vectors to smooth paths passing through a point on the manifold. A vector \(x^\mu\) at a point \(p \in M\) can be defined as the derivative of a path \(\gamma: [0, 1] \to M\), taken in the natural way (partial derivatives in each coordinate function). The set of all tangent vectors at a point \(p\) is called the tangent space at p, \(T_p M\); the disjoint union of all tangent spaces on the manifold is the tangent bundle, \(TM\). Next, we introduce forms as linear maps that take a vector and return a scalar (algebraic dual to vectors). A form \(\omega: T_p M \to \mathbb{R}\) linearly maps vectors in a tangent space to scalars, and can also be denoted locally as \(\omega_\mu\). The set of all forms at a point \(p\) is the cotangent space at p, \(T_p^* M\); the disjoint union of all cotangent spaces on the manifold is the cotangent bundle, \(T^* M\). Last, we introduce the metric \(g\) on our manifold first globally, as a map taking two vector fields and producing a smooth function: \(g: \mathfrak{X}(M) \times \mathfrak{X}(M) \to C^\infty(M)\). Equivalently, the metric can be defined locally in terms of component functions. More often in physics, though, we define the metric in terms of the line element \(ds^2\) or distance squared between two infinitesimally separated points, \(ds^2 = g_{\mu\nu} dx^\mu dx^\nu\).
Connections and Derivatives. After looking at various smooth objects on the manifold, we next need to introduce ways of taking derivatives more generally. We began with the familiar partial derivative with respect to a coordinate function, \(\partial_\mu \equiv \partial/\partial x^\mu\). In order to generalize this definition to handle curvature, we first needed to introduce ways of comparing objects defined at different points on the manifold: a connection between these object spaces. There was detailed discussion around two related ways of doing this: defining a connection on the tangent bundle, or defining a connection on the manifold (though one can be derived from the other). We’ll briefly summarize here in terms of the manifold connection. A connection \(\nabla\) on the manifold \(M\) is a map \(\mathfrak{X}(M) \times \mathfrak{X}(M) \to \mathfrak{X}(M)\), equivalently \((X, Y) \mapsto \nabla_X Y\), with the following properties given \(X, Y \in \mathfrak{X}(M)\) and \(f \in C^\infty (M)\): (1) the connection is \(f\)-linear in its first argument \(\nabla_{(fX)} = f\left(\nabla_X Y \right)\), and (2) obeys a \(f\)-Leibniz identity in the second argument \(\nabla_X (fY) = \left(\partial_X f\right)Y + f \left(\nabla_X Y\right)\). In physics, we are often interested in the (unique) Levi-Civita connection, which has the additional two properties: (1) metric compatibility \(\nabla g = 0\) and (2) torsion-free condition \(\nabla_X Y – \nabla_Y X = [X, Y] \equiv \mathcal{L}_X Y\). Locally, the components of the connection can be expressed using Christoffel symbols \(\Gamma_{ij}^k\), where the connection components relate via \(\nabla_i e_j = \Gamma_{ij}^k e_k\) for some basis \(\{e_k\}\). These connection components can be used to define the covariant derivative \(\nabla_\mu\) for arbitrary tensors. For example, the covariant derivative for a vector is \(\nabla_\mu v^\nu \equiv \partial_\mu v^\nu + \Gamma_{\mu\lambda}^\nu v^\lambda\). Last we introduce the Lie derivative with respect to a vector field $X$, which is the natural Riemannian derivative along the flows induced by the vector field, component-wise. For the metric, the Lie derivative is in general: \(\mathcal{L}_X g = X^c \nabla_c g_{ab} + g_{cb}\nabla_a X^c + g_{ac} \nabla_b X^c\). Note for the Levi-Civita connection, this simplifies to \(\mathcal{L}_X g = \nabla_a X_b + \nabla_b X_a\).
Killing Equation and Killing Vectors. Next, we introduce Killing vectors, as they will be essential in classifying spacetimes based on symmetries. At a high-level, Killing vector fields generate the symmetries, as the flows generated are isometries of the manifold. This means that transporting any object along these flows will not distort distances on the object, and can be succinctly stated by the vanishing of the Lie derivative of the metric. A vector field \(K \in \mathfrak{X}(M)\) is a Killing vector if it satisfies \(\mathcal{L}_K g = 0\), or expressed locally for the Killing vector \(K^\mu\), \(\nabla_\mu K_\nu + \nabla_\nu K_\mu = 0\). For example, Minkowski space has many symmetries (Poincare group). The specific Killing vectors are: (a) 3 space translations \(\{ \partial_x, \partial_y, \partial_z \}\), (b) 1 time translation \(\{ \partial_t \}\), (c) 3 spatial rotations \(\{ -y\partial_x + x\partial_y, -z\partial_y + y\partial_z, -x\partial_z + z\partial_x \}\), and (d) 3 boosts (changes in frame velocity, seen as rotating space and time) \(\{ x\partial_t + t\partial_x, y\partial_t + t\partial_y, z\partial_t + t\partial_z \}\).
Petrov Classification
Having made it through the speed-run through necessary differential geometry (again, to be read in more detail together in the summer), we discussed the primary point of the focus session: using Killing vectors to classify all possible 4-D spacetimes according to their symmetries. As an aside, a 4-D spacetime will have at most 4 linearly independent Killing vectors (up to multiplicity). This can be seen by looking at pairs of Killing vectors as solutions to the bivector eigenvalue problem in terms of the Weyl tensor $$C_{abcd}$, which can be stated as \(\frac{1}{2}C^{ab}{}_{mn}X^{mn} = \lambda X^{mn}\). We list the Petrov classes below in terms of multiplicities of linearly independent Killing vectors (principal null directions, PND) and give physical interpretation, where 3 principal null directions with multiplicity 2 would be denoted 3m2, .
- Type I: 4m1. Physically: combo of all types, typically too asymmetric to be useful.
- Type II: 1m2 + 2m1. Physically: combo of Type N and Type III
- Type D: 2m2. Physically: isolated massive object (ingoing/outgoing radial geodesics), e.g. black hole.
- Type III: 1m3 + 1m1. Physically: longitudinal gravitational radiation (tidal shearing), often neglected.
- Type N: 1m4. Physically: transverse gravitational radiation (gravitational waves), the Killing vector is the wave vector.
- Type O: Weyl tensor vanishes. Physically: conformally flat (no distant objects exerting impact on local regions)
Example: FLRW Cosmology
We then introduced a sample model of cosmology used as a “starting point” for a large portion of modern cosmological models.
Model and Metric. The FLRW model, named after its creators Freedman, Lemaitre, Robertson, and Walker, is a maximally symmetrical in space, though not in time. It is constructed by assuming homogeneity and isotropy, which will be discussed further below. The metric for FLRW can be given as \(ds^2 = -dt^2 + a^2(t) d\Sigma^2\), where \(d\Sigma^2\) is the spatial metric. It is often stated in reduced circumference spherical coordinates, \(d\Sigma^2 = 1 / (1 – kr^2) dr^2 + r^2 d\Omega^2\). The function \(a(t)\) measures spatial scale as a function of time, and is related to the Hubble parameter \(H(t) \equiv \dot{a} / a\).
Application to Homogeneity. We now examine the term homogeneous as applied to cosmological models. In our reading of group theory, we discussed the concept of group actions and orbits of elements. If a group \(G\) acts on a set \(A\), then the set of cosets (or orbits) form a partition of \(A\). Recall, a coset of an element \(a \in A\), is given as \(aG = \{ga : g \in G\} \subset A\). The set \(aG \subset A\) is called the orbit of \(a\) in \(G\), and can be though of as “where the group \(G\) can take the element \(a\) in the set \(A\)”. We can define an equivalence relation using these cosets, by deeming two elements of \(A\) to be equivalent if they belong to the same coset. Equivalently, this implies that if \(a \sim b\) then there exists \(g \in G\) such that \(b = ga\). If the group action is transitive, then all cosets are equivalent and the former statement holds for all \(a, b \in A\). In such a case, all elements of \(A\) are similar, and \(A\) can be said to be homogeneous. This is the sense in which a cosmological model can be homogeneous; the symmetry group of the model must act transitively on the spacetime manifold.
Application to isotropy. We now examine the term isotropic as applied to cosmological models. In our reading of group theory, we discussed the concept of stabilizers, or subsets of a group that when acting on an element \(a\) leave it unchanged, or fixed. At each point \(p\) on the spacetime manifold \(M\), it is possible to define the isotropy group as the stabilizer of that point, which will be the subgroup of isometries that leave the point fixed. The most common example is rotations about axes intersecting the point \(p\). We say that a point \(p\) in spacetime is isotropic if the isotropy group is nontrivial, and that a spacetime is isotropic if all points are isotropic. Note, if a spacetime is homogeneous with at least one isotropic point, then the whole spacetime is isotropic.
Up Next:
Reading Group:
For next week’s reading we aim to be complete:
- Lee: 3
- Dummit & Foote: 4
Interesting or Relevant Talks:
- Colloquia